Takie pytanie podobno otrzymali na początku XVIII wieku uczniowie klasy, do której chodził Carl Friedrich Gauss (nazywany Księciem Matematyki, ze względu na wybitne osiągnięcia nawet już w młodym wieku).

Dodawanie ich po kolei (w tamtych czasach oczywiście bez kalkulatora!) na pewno było żmudnym zadaniem i ja bym zapewne się znudziła przed połową. Młodziutki Gauss podobno zaskoczył nauczyciela szybko wyliczoną odpowiedzią.

Carl zauważył pewną prawidłowość: jeśli będzie dodawał liczby pierwszą z ostatnią, drugą z przedostatnią itd., to zawsze będą się one sumowały do 101.

   

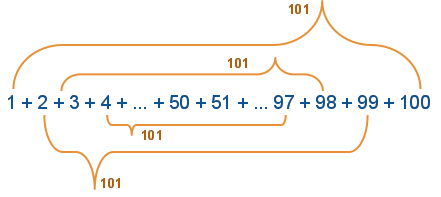
Uwaga, gdy liczba składników jest nieparzysta, środkowa liczba nie będzie miała różnej od siebie pary, tylko będzie podwajana, np. dla sumy od 1 do 5 zachodzi:

   

W związku z tym, łatwiejszym sposobem, który zawsze działa, jest dodanie do siebie liczb podwójnie, a potem podzielenie wyniku przez 2.

Gdy doda się do siebie cyfry od 1 do 100 dwa razy (zapisując je pod sobą raz od przodu, raz od tyłu), to 100-krotnie doda się do siebie liczbę 101, czyli uzyska wynik 10100.

   

   

   

   

To nie koniec, bo jeszcze w związku z tym, że to samo dodawaliśmy dwukrotnie, trzeba ten wynik podzielić przez 2. Ostatecznie suma liczb od 1 do 100 to 5050.

A teraz trudniejszy przykład dla chętnych. Obliczmy sumę liczb parzystych od 1 do 100. Liczb parzystych z tego przedziału jest 50, a pierwsza z nich to 2. Rozumując podobnie jak Gauss otrzymujemy:

   

Ćwiczenia

Oblicz sumy liczb:

1. 1. od 1 do 200
   2. podzielnych przez 3 (między 1 a 100)
   3. nieparzystych (między 1 a 100)

1.  

Odpowiedzi

1. Suma liczb od 1 do 200 to 20100
2. Suma liczb nieparzystych od 1 do 99 to 2500
3. Suma liczb podzielnych przez 3 od 3 do 99 to 1683