
Lis, kura i ziarno
W jaki sposób rolnik może przewieźć lisa, kurę i worek ziarna na drugą stronę rzeki, jeśli łódka mieści oprócz niego tylko jedną rzecz/pasażera oraz lis nie powinien zostać sam na sam z kurą, a kura z ziarnem?1. Przewozi kurę
2. Wraca sam
3. Przewozi lisa
4. Wraca z kurą
5. Przewozi ziarno
6. Wraca sam
7. Przewozi kurę
Podobnie jak w rozwiązaniu #1, ale przewozi ziarno w kroku 3, a lisa w kroku 5.

Wiaderka
Jak dysponując dwoma wiaderkami o pojemności 5l i 3l odmierzyć dokładnie 4 litry wody?Napełnić 3-litrowe naczynie, przelać zawartość do 5-litrowego, znów napełnić naczynie 3-litrowe, dolać do naczynia 5-litrowego brakujące 2 litry, wtedy w naczyniu 3-litrowym zostaje 1 litr, następnie wylać zawartość naczynia 5-litrowego i przelać do niego litr z drugiego naczynia, na koniec napełnić ponownie naczynie 3-litrowe i dolać do naczynia 5-litrowego, wtedy jest w nim 4 litry (zmarnowaliśmy w procesie 5l wody)
Napełnić 5-litrowe naczynie, przelać ile się da do naczynia 3-litrowego, wtedy w 5-litrowym zostają 2 litry, wylac zawartość naczynia 3-litrowego i przelać tam zawartość 5-litrowego, czyli 2l, następnie napełnić naczynie 5-litrowe i dolac do 3-litrowego ile się da, czyli 1 litr, wtedy w naczyniu 5-litrowym zostają 4 litry (zmarnowaliśmy w procesie 6l wody)

Szymon i Tymon
Dwa lata temu Szymon był trzy razy starszy od Tymona, a za trzy lata Tymon będzie dwa razy młodszy od Szymona. Ile mają lat?
Szymon ma 17 lat, a Tymon 7.
Wystarczyło rozwiązać układ równań:
x-2=3(y-2)
x+3=2(y+3)
gdzie x to wiek Szymona, a y to wiek Tymona.
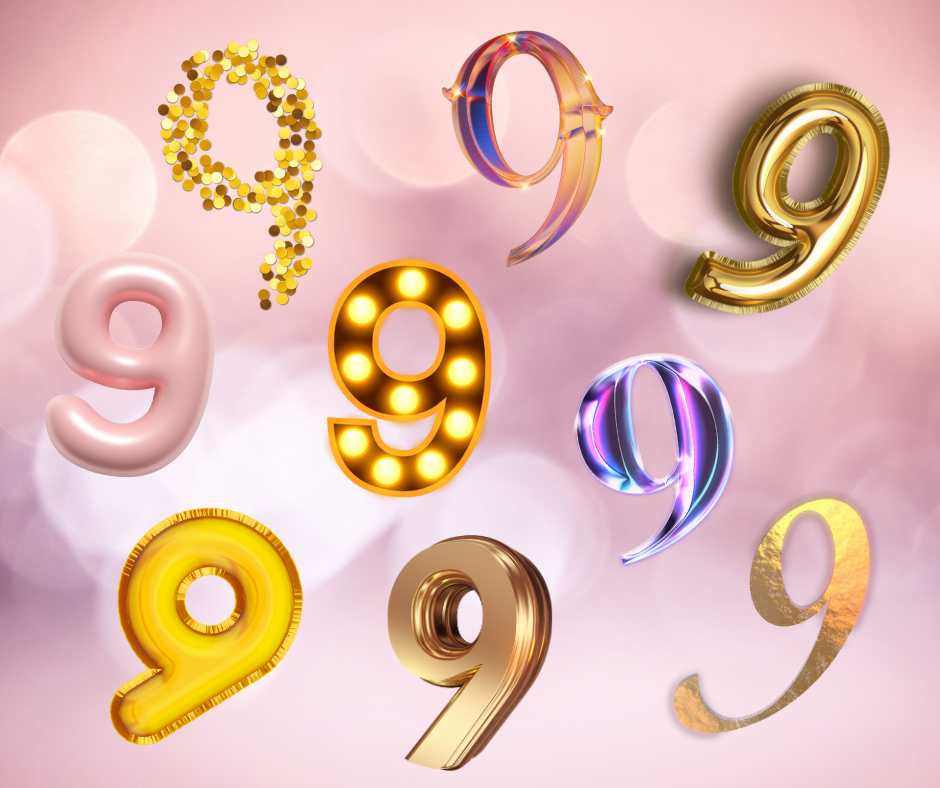
Dziewiątki
Uczeń zapisuje w zeszycie liczby od 1 do 100. Ile razy napisze cyfrę 9?
20 razy
Cyfra 9 występuje 10 razy jako cyfra jedności (9,19,…,99) i 10 razy jako cyfra dziesiątek (90-99).

Kolorowe kule
W pudełku są kule czerwone, niebieskie i żółte. Trzy z nich nie są czerwone, cztery nie są niebieskie, a pięć nie jest żółtych. Ile jest kul?
Jest 6 kul: 3 czerwone, 2 niebieskie i 1 żółta.

Klepsydry
- Jak przy pomocy dwóch klepsydr, 7-minutowej oraz 11-minutowej, można odmierzyć 15 minut?
- Jak przy pomocy dwóch klepsydr, 5-minutowej oraz 8-minutowej, można odmierzyć 12 minut?
W obu przypadkach chodzi o rozwiązanie, w którym:
– obracanie klepsydry nie zabiera czasu, jest natychmiastowe,
– nie da się dokładnie ustalić, kiedy przesypała się połowa czy inna część piasku,
– odmierzamy czas bez żadnych przerw w trakcie,
– im wcześniej zaczniemy odmierzać czas tym lepiej (bo się spieszymy)
– równocześnie obracam obie klepsydry
– gdy skończy się przesypywac klepsydra 7-minutowa od razu ją obracam (minęło 7 min)
– gdy skończy się przesypywac klepsydra 11-minutowa, to 7-minutowa zdążyła odmierzyć kolejne 4 minuty (minęło łącznie 11 min)
– obracam ją, żeby odmierzyła ponownie 4 minuty (minęło łącznie 15 min)
– równocześnie obracam obie klepsydry
– gdy skończy się przesypywac klepsydra 5-minutowa od razu ją obracam (minęło 5 min)
– gdy skończy się przesypywac klepsydra 8-minutowa, obracam ją, a 5-minutowa zdążyła odmierzyć kolejne 3 minuty, zostawiam ją, żeby odmierzała dalej (minęło łącznie 8 minut)
– gdy skończy się przesypywac klepsydra 5-minutowa, to 8-minutowa zdążyła odmierzyć w tym czasie kolejne 2 minuty (łącznie minęło 10 minut)
– obracam ją, żeby odmierzyła ponownie te 2 minuty (minęło łącznie 12 min)

Ludzie i konie
W stajni są 22 głowy i 72 nogi. Ile jest koni, a ile ludzi?
14 koni i 8 ludzi

Jaki dzień
Jeżeli przedwczorajsze jutro jest w niedzielę, to jaki dzień będzie dwa dni po dzisiejszym pojutrze?
Piątek

Skarpetki
W szufladzie jest 10 skarpetek czarnych, 8 szarych i 6 białych.
- Ile skarpetek minimum trzeba wyciągnąć, jeśli chcemy ubrać białą parę, a nic nie widać w ciemności?
- 2. A jeśli chcemy jakąkolwiek parę (po prostu chcemy dwie w tym samym kolorze)?
Zakładamy, że nie ma podziału na skarpetki lewe i prawe, wszystkie są takie same.
20 skarpetek
(bo jeśli będzie 19, to może się okazać, że będą wylosowane same czarne i szare skarpetki i tylko jedna biała, natomiast przy 20 w każdym możliwym przypadku będą co najmniej 2 białe)
4 skarpetki
(jeśli byłyby 3, to mogłaby być każda w innym kolorze, przy 4 na pewno jakaś para się trafi)

W górach
Asia, Basia i Kasia rozmawiają o górach. Dwie z nich były w Karpatach, dwie w Sudetach i dwie w Górach Świętokrzyskich. Basia nie była w Karpatach ani Sudetach, a kto nie był w Górach Świętokrzyskich, nie był również w Karpatach. Kto gdzie był?
Asia i Kasia były zarówno w Karpatach, Sudetach jak i Górach Świętokrzyskich, a Basia nie była w żadnych z tych gór.
Wyjaśnienie:
Gdyby Asia nie była w Górach Świętokrzyskich, to nie byłaby też w Karpatach, zgodnie z założeniem. Wtedy ani Asia ani Basia nie byłyby w Karpatach, czyli byłaby tam tylko Kasia. Ale przecież po dwie osoby były w każdym paśmie, więc byłaby to sprzeczność. To samo rozumowanie mozna przeprowadzić dla Kasi. Stąd Asia i Kasia musiały być w Górach Świętokrzyskich, a skoro były tam tylko 2 osoby, to Basia nie. Więc Basia nie była w żadnych górach (bo w innych też nie była z założeń zadania), a w takim razie Asia i Kasia musiały być wszędzie (żeby było po 2 osoby).

Karty
Z talii 52 kart niektóre się zgubiły. Gdybyśmy teraz chcieli rozdać wszystkie karty po równo 4 osobom, zostaną 3 karty reszty, a jeśli 3 lub 5 osobom – zostaną 2 karty reszty. Ile jest kart?
47 kart

Ojciec i syn
Ojciec i syn mają razem 66 lat. Gdy zamienimy kolejnością cyfry wieku ojca, otrzymamy wiek syna. Ile lat ma każdy z nich?
Tym razem łamigłówka była podchwytliwa, bo miała więcej niż jedną odpowiedź ![]()
42 i 24
51 i 15
60 i 6 (ten przypadek jest dyskusyjny, ale specjalnie napisałam, że się zamienia kolejnością cyfry wieku ojca, a nie odwrotnie).
Przykładowe rozwiązanie:
Zakładam, że x to pierwsza cyfra wieku ojca, a y druga. Wtedy wiek ojca to 10x+y, a syna 10y+x. Stąd:
10x + y + 10y + x = 66
11x + 11y = 66
x + y = 6
Z założeń zadania x i y to cyfry, więc liczby naturalne i jeszcze x>=y, bo ojciec nie może być młodszy. Odpada rozwiązanie (3,3) z przyczyn biologicznych ![]() Więc mamy 3 rozwiązania: pary (6,0), (5,1) oraz (4,2) co daje wiek jak wyżej.
Więc mamy 3 rozwiązania: pary (6,0), (5,1) oraz (4,2) co daje wiek jak wyżej.

Prezent
10 znajomych chciało złożyć się na prezent. Niestety dwójka z nich zrezygnowała, więc pozostali musieli dołożyć po 10 zł. Ile kosztował prezent?
400 zł

Ślimak
Ślimak wspina się na drzewo. Każdego dnia pokonuje 8m w górę, a w nocy zsuwa się 6m w dół. Kiedy dotrze do wierzchołka drzewa o wysokości 16m?
[Źródło łamigłówki: “Zagadki matematyczne” Krzysztofa Ciesielskiego i Zdzisława Pogody]
Po 5 dniach
Pierwszego dnia dotrze do 8m, a każdego kolejnego dnia będzie tylko o 2m wyżej, bo w nocy się zsuwa się o 6m. Czyli drugiego dnia dotrze do 10m, trzeciego 12m i tak dalej, więc 16m osiągnie piątego dnia.

Trzy liczby
Jakie 3 liczby naturalne dają ten sam wynik, niezależnie od tego czy się je mnoży czy dodaje?
Są dwa rozwiązania w liczbach naturalnych ![]()
0, 0, 0
1, 2, 3

Znajdź liczbę
Jaka jest najmniejsza liczba całkowita dodatnia równa siedmiokrotności sumy jej cyfr?
21
Szukamy NAJMNIEJSZEJ liczby naturalnej dodatniej, która spełnia powyższą zależność. Czy może to być zatem liczba jednocyfrowa? Musiałaby być ona jednocześnie swoją siedmiokrotnościa. Tak jest tylko w przypadku zera, ale specjalnie napisałam, że szukamy liczby dodatniej, żeby nie było za łatwo ![]()
Załóżmy dalej, że istnieje taka liczba dwucyfrowa. Niech x oznacza jej cyfrę dziesiątek, a y cyfrę jedności. Wtedy chcemy, żeby zachodziło:
10x + y = 7(x+y)
3x = 6y
x = 2y
Pamiętajmy, że x i y to cyfry dodatnie. Równanie to ma wtedy 4 rozwiązania. Najmniejszą liczbę daje para x=2 i y=1.

Kule w pudełkach
Jeśli będę wkładać po jednej kuli do przygotowanych pudełek, braknie mi jednego pudełka, a jeśli będę wkładać po dwie, to będzie o jedno za dużo. Ile mam kuli i pudełek?
4 kule, 3 pudełka ![]()
Można sobie rozwiązać na przykład układem równań.
x – liczba kuli
y – liczba pudełek
x = y+1
1/2 x = y-1

Wstaw znaki
Na tablicy jest napisany ciąg 123456789. Wstaw pomiędzy cyfry znaki +, – lub nic, tak żeby suma wynosiła 100.
(Jeśli między cyframi nic nie wstawimy, to sklejamy je w jedną liczbę, np. 34, 123)
1+2+34-5+67-8+9
123-4-5-6-7+8-9
123+45-67+8-9
123+4-5+67-89
1+2+3-4+5+6+78+9
12+3+4+5-6-7+89
12-3-4+5-6+7+89
Jak widać trochę tych możliwości jest, a być może to jeszcze nie wszystkie ![]()

Cukierki
Jaś i Staś dzielili się cukierkami. Ten, który miał ich więcej, oddawał bratu tyle cukierków, ile aktualnie miał ten brat. Po dwóch takich wymianach (najpierw dzielił się Jaś, a potem Staś) każdy miał po 4 cukierki. Po ile mieli ich na początku?
Jaś – 5, Staś – 3
Niech x oznacza początkową liczbę cukierków Jasia, a y Stasia.
Po pierwszej wymianie mamy następujące liczby cukierków:
J: x-y
S: 2y
Po drugiej wymianie:
J: 2(x-y)
S: 2y-(x-y)=3y-x
Po drugiej wymianie były po 4 cukierki, stąd mamy układ równań
2(x-y)=4
3y-x=4
którego rozwiązaniem jest para x=5, y=3

Jabłka i gruszki
W koszyku jest 8 gruszek i kilka jabłek. Każdy z tych owoców jest albo cały zielony, albo cały żółty. Jabłek jest o 3 więcej niż owoców zielonych, a żółtych gruszek jest sześć. Ile żółtych jabłek jest w tym koszyku?
[Źródło łamigłówki: https://www.kangur-mat.pl]
5 żółtych jabłek
Oznaczmy:
a – jabłka zielone
b – jabłka żółte
c – gruszki zielone
d – gruszki żółte
Z informacji podanych w zadaniu mamy:
c + d = 8
a + b = a + c + 3
d = 6
Z tego wynika:
c = 2
b = 5

Zwierzęta na łące
Na łące pasą się krowy, owce i gęsi. Wiemy, że 10 ze zwierząt nie jest krowami, 8 nie jest owcami, a gęsi stanowią 20% wszystkich zwierząt. Po ile zwierzaków z każdego gatunku pasie się na łące?
5 krów, 7 owiec, 3 gęsi
x – liczba krów
y – liczba owiec
z – liczba gęsi
y + z = 10
x + z = 8
5z = x + y + z
x + y = 18 – 2z
x + y = 4z
18 – 2z = 4z
6z = 18
z = 3
y = 7
x = 5

Wanna
W wannie są dwa krany. Gdy użyjemy tylko pierwszego z nich, wanna napełni się w 15 min, a gdy drugiego – w 10 min. Po jakim czasie wanna napełni się, gdy użyjemy obu naraz?
6 minut
Przykładowe sposoby rozwiązania:
1. Przeliczamy ile wanien byłoby napełnionych w godzinę: pierwszy kran napełniłby 4, a drugi 6, więc razem 10. 10 wanien w 60 minut, więc jedna w 6 minut.
2. W minutę zostaję napełnione odpowiednio 1/15 i 1/10 wanny, więc razem 1/6 wanny. W związku z tym, żeby otrzymać całą wannę, potrzebujemy 6 minut.

Jajka
Na stole jest 9 jajek. Wiemy, że 8 z nich waży dokładnie tyle samo, a jedno jest nieznacznie cięższe od reszty. Jak można ustalić które to, dwukrotnie używając wagi szalkowej (bez używania odważników)?
Uwaga: Mamy tylko dwa ważenia i mamy mieć pewność, że jajko jest cięższe. Od razu zaznaczam, że ważenie w rękach na oko odpada ![]() Załóżmy, że różnica jest minimalna.
Załóżmy, że różnica jest minimalna.
1 ważenie
Grupuję jajka po 3 i kładę na wadze 2 losowo wybrane grupki. Jeśli któraś grupa jest cięższa, do kolejnego ważenia biorę tylko ją, bo wśród nich na pewno musi być to cięższe jajko. Jeśli waga była równa, to wiadomo, że cięższe jajko jest w trzeciej (nieważonej) kupce i wtedy wybieram ją.![]()
![]()
![]()
2 ważenie
W kolejnym kroku powtarzam w analogiczny sposób procedurę, tym razem kładąc na szalkach po jednym jajku spośród wybranej trójki. Rozumuję podobnie jak w pierwszym kroku i voila! cięższe jajko znalezione![]()
