Co odsiewa sito Eratostenesa? ⋆ Matematykini

Czytając matematyczną literaturę, czasami można się natknąć na różne ciekawe obiekty, np. dywan (Sierpińskiego), wstęga (Mobiusa), butelka (Kleina), pierścień (Gaussa) czy łańcuch (Markowa). Dziś na warsztat weźmiemy sito, a konkretnie sito Eratostenesa.

Wszelkiego rodzaju sita i sitka charakteryzują się tym, że oddzielają od siebie pewne obiekty, mają otwory, które przepuszczają mniejsze cząsteczki, a zatrzymują większe.

Sito Eratostenesa odsiewa liczby złożone, a zostawia liczby pierwsze. Nazwa pochodzi od Eratostenesa z Cyreny, który żył na przełomie III i II wieku p.n.e.

**Eratostenes z Cyreny**
Źródło: Wikipedia

Sito Eratostenesa to algorytm znajdowania liczb pierwszych mniejszych od danej liczby.

Przypomnę, jeśli nie pamiętasz, że liczby pierwsze to takie, które są podzielne tylko przez siebie i przez 1, wiec są one pod tym względem specjalne (oto kilka pierwszych liczb pierwszych: $2, 3, 5, 7, 11, \ldots$ ).

Dla przykładu, jak szybko znaleźć liczby pierwsze mniejsze od $100$ ? Przy małych liczbach jeszcze jest łatwo sprawdzić, przez co się dzielą, ale jak na przykład dowiedzieć się, czy taka liczba $97$ jest pierwsza???

Oczywiście można szukać wszystkich dzielników pojedynczo dla każdej liczby, ale po co, skoro można to szybko zrobić hurtowo.

Algorytm wygląda następująco (dla dowolnej liczby $n$ ):

Wypisuję liczby od 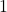$1$ do $n$
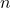
Skreślam jedynkę
Wybieram najmniejszą nieskreśloną liczbę i wykreślam wszystkie jej wielokrotności większe od niej
Powtarzam powyższy krok aż liczba, której wielokrotności wykreślamy, przekroczy $\sqrt{n}$
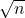
Nieskreślone liczby to wszystkie liczby pierwsze mniejsze od $n$

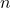
Powyżej został podany przepis, zastosujmy go teraz w praktyce:
– wypisuję liczby od $1$ do $100$
– wykreślam jedynkę
– najmniejsza nieskreślona jest dwójka, wykreślam jej wielokrotności, skacząc co $2$ , czyli: $4, 6, 8, 10, \dots, 98, 100$
– najmniejszą nieskreśloną jest trójka, więc wykreślam jej wielokrotności: $6, 9, 12, \ldots , 96, 99$
– czwórka już jest skreślona, idę dalej
– kolejna jest piątka, więc wykreślam: $10, 15, 20, \ldots, 95, 100$
– szóstka już jest skreślona, idę dalej
– kolejna jest siódemka, więc wykreślam: $14, 21, \ldots, 91, 98$
– ósemka, dziewiątka i dziesiątka są już skreślone, idę dalej
– kolejna jest $11$ , jest większa niż $\sqrt{100}=10$ , więc kończę procedurę
– niewykreślone są: $2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97$ – są to liczby pierwsze

Wyjaśnienia dla dociekliwych:
– skreślamy wielokrotności danej liczby $k$ , bo mamy pewność, że nie są one pierwsze (gdyż są podzielne przez tę liczbę $k$ )
– pomijamy liczby już wykreślone, bo skoro są wykreślone, to dzielą się przez jakąś liczbę $k$ , więc na pewno wszystkie jej wielokrotności też już zostały wykreślone przy okazji $k$ (np. dla szóstki, już przy krokach dla $2$ oraz dla $3$ wykreśliliśmy wszystkie wielokrotności $6$ , czyli $12, 18, \ldots, 96$ )
– kończymy algorytm na $\sqrt{100}=10$ , bo jeśli jakaś liczba byłaby podzielna przez liczbę większą od $10$ , to też musiałaby mieć dzielnik mniejszy niż $10$ (więc już jest skreślona); gdyby tak nie było, to oba dzielniki, które po wymnożeniu dają tę liczbę, byłyby większe od $10$ , więc ta liczba musiałaby być większa niż $100$ , a nas interesują liczby od $1$ do $100$ ; dla przykładu, nie muszę wykreślać wielokrotności $11$ , bo wszystkie liczby $22, 33, 44, \ldots, 99$ już zostały skreślone przy okazji $2, 3, 4, \ldots, 9$ odpowiednio, a liczba $11\cdot 10=110$ już jest poza naszym zakresem